Can someone answer this for me?
| Can someone answer this for me?09-02-2015 16:43 | |
| campy☆☆☆☆☆ (8) |
I am new to the forum and I am in the group of skeptics on MAN MADE global warming. I don't disagree that the earth is warming, but I would say it's been getting warmer ever since the earth was a snow ball millions or billions years ago. The question I have that no one has been able to answer is " What's the proper temperature should the earth be?" Does the settled science tell us what it is? How can you say it's too warm if you don't have the answer to that? |
| 09-02-2015 17:42 | |
| greyviper☆☆☆☆☆ (44) |
well, there's really no baseline temperature for that most likely. in my subjective opinion, anything hotter than 20-25 degrees celsius. |
| 09-02-2015 19:06 | |
| campy☆☆☆☆☆ (8) |
Why is there no baseline temperature? How can you say one way or another without that. |
| 09-02-2015 19:37 | |
| greyviper☆☆☆☆☆ (44) |
Its because no baseline was established in the first place. For me, room temperature would be a good start though. |
| 10-02-2015 01:53 | |
Abraham3 ★★☆☆☆(256) |
As I told you in another forum here, the problem is not the absolute temperature the Earth will reach, the problem is the rate at which it is changing. |
| 10-02-2015 02:36 | |
| greyviper☆☆☆☆☆ (44) |
Abraham3 wrote: Yes, certainly. I do agree with the statement. You cannot measure the absolute temperature but only the delta T i.e. the change in temperature or the rate of change. It just came to my mind that you could use calculus for this computations... |
| 10-02-2015 04:37 | |
| Abraham3★★☆☆☆ (256) |
I'm sorry, but that is not what I meant at all. We can most certainly measure the absolute temperature. That is not the issue. Humans and all life on this planet could exist quite happily over a fairly wide range of temperatures. What we cannot do well with are changes in our climate that happen too rapidly for us to easily adapt. That is what we are currently undergoing. And, yes, I'm sure calculus will be involved but I really don't know what computations you're talking about. |
| 10-02-2015 17:41 | |
| greyviper☆☆☆☆☆ (44) |
Abraham3 wrote: Yes, that is exactly what happens. The changes in the temperature are happening too fast that I could certainly notice it. An evidence of that is I can feel the summer getting hotter and hotter every year. Of course, organic life can still adapt but there would be a number of consequences. With regards to computations I guess that would the rate of change as to how fast the temperature rises. Some areas would probably be cooling, some would be increasing in temperature. The world is round after all and its a matter of movement of heat from one point of the earth to another. Edited on 10-02-2015 17:42 |
| 12-02-2015 10:21 | |
| Cornelius☆☆☆☆☆ (17) |
Hey Campy, Good question really. Hard one to put any real answer on that is a figure if that is what you are looking for. But simply put....it would have to be within a temperature range that can support life. And by life......I mean from micro-organisms to plants of a great diversity, to animals, insects, to sea life and then humans. Humans lastly, because all of the others things mentioned are the infrastructure (when they are allowed to do the role that they naturally do) that supports our life. So it makes sense to love and look after those that are looking after us. The temperatures that we talk about are all based on air temperature...or ambient air....and measured in the shade. The temperature in direct sunlight is far hotter. So if you sit under a shady tree on a hot day, and then step out of the shade and sit in the sun, it you will become affected by it far quicker to the point that you will have to go back to the shade, or risk sunburn, heatstroke and possibly death. You are dealing with Radiant heat in this case or sunlight made up of infrared rays. It is the same for the environment and the associated creatures in the living system. When you take away the forest, you expose the ground before that was previously protected and cool which was in the temperature range that that is required to support their life, to now......super hot. The smaller insects and micro organisms fry. The smaller ones were supporting the larger ones. Their shelter, water and food source has become extinct. And soon they do to. A possible indication of what our future may be unless we humans less stubborn and open ourselves up to accepting change. This de-forestation, of which the main offender is animal agriculture industry(animals for human consumption), which occupies between 30- 45% of the Earths total land, effectively has put our living system under extreme stress, by not only removing their habitat and forcing many into extinction (so now what they use to do in the living system has died too), but also exposing the Earths surface to far hotter Radiant temperatures compared to the Ambient temperatures that they have always been use to when the trees were protecting it. In fact 70% of former forest in the Amazon has been turned over to pasture for grazing. A hub area of our global life system. https://cgspace.cgiar.org/bitstream/handle/10568/10601/IssueBrief3.pdf http://www.un.org/apps/news/story.asp?newsID=20772 The ground, being a great absorber of thermal mass, is obviously going to get a whole lot hotter too and radiate that heat back into the atmosphere. I find it interesting, that the human body is made up of approx. 70% water. That the Earth is 70% water. The average healthy human body core temperature is 37 degrees. It is fatal down to 20 degrees and fatal up to 41. Water has high specific heat properties. Meaning the amount of heat needed to raise the temperature a specific amount. One of waters most specific properties is that it takes a lot of heat to get it to move upwards in temperature. As we have seen with the human body, only 4 degrees change in a hotter direction is fatal. If this works the same with the oceans waters that are already on the rise, how much time do we have to sort out this problem? Not a lot it would seem. |
| 13-02-2015 00:56 | |
| Abraham3★★☆☆☆ (256) |
Cornelius wrote: I disagree. I believe the question is completely rhetorical. It is a common denier tactic intended to imply that we are not justified in assuming climate change bad if we don't know what temperature would be best. It is often partnered with arguments of all the "good" that an increase in temperatures and CO2 levels will bring (increased crop growth and more pleasant conditions in high latitudes). Cornelius wrote: As has been pointed out repeatedly, the threat of global warming is not the absolute values global temperatures will reach but the rate of change. Cornelius wrote: The average global temperature includes air temperatures from the surface of the Earth to the Stratopause and from the ocean's surface to it's bottom; those temperatures all weighted for the masses involved. Your comments here about in and out of the shade are more senseless rambling. "Air temperature", by definition, is a measurement of the air and not of how hot our thermometers can get when left in direct sunlight. Cornelius wrote: Nonsense. Virtually every watt of solar infrared (IR or "radiant heat") is absorbed by the various GHGs in the Earth's atmosphere long before they would hit us. The vast majority of solar electromagnetic radiation (EMR) that makes it to the Earth's surface and our skin is in the visible and UV spectra. The IR we receive is all secondary, radiated by matter around us that has been heated by absorbing the EMR that did make it through. Cornelius wrote: The major climatic effect of deforestation is the loss of plant life that absorbed carbon dioxide and emitted oxygen - thus further increasing the rate at which atmospheric CO2 levels grow. The same amount of solar energy is falling on the bare ground that once fell on top of whatever flora was once present. In fact, many (but certainly not all) instances of deforestation produce a more reflective surface (light colored sand vice deep green canopy, for instance) and thus, through an increase of albedo, DECREASE the amount of solar energy directly absorbed. Cornelius wrote: Deforestation is a direct loss of habitat. The effects on macro-organisms is a great deal more direct than a loss of microorganisms. And these things do not fry in the sun as you've twice now suggested. They simply die of UV exposure (in the case of some microorganisms), lack of water and lack of food: increased competition for a shrinking set of resources as they are forced into smaller and smaller habitats. Many insects and microorganisms have enormous tolerance to temperature changes. Cornelius wrote: I admit that eating plant protein is a far more efficient use of land than is the consumption of animal proteins and thus were all humans to cease eating grazing animals, the area required to replace the protein they supplied would be a tenth what they once needed. However I have to point out that agriculture, exclusive of livestock, lags only slightly in terms of land use and that land areas being used for monocultured crop species - and typically treated both with fertilizers and pesticides (or even with broad-spectrum herbicides on resistant GMO crops) are no better for the well being of wildlife or the maintenance of diverse habitats - and are arguably much worse - than a far less controlled and less toxic field grazed on and fertilized by livestock. Addtionally, as I pointed out above, deforestation does not significantly enhance global warming through albedo change, but through the loss of a capacity to convert carbon dioxide to oxygen. Cornelius wrote: You need to keep in mind that energy, like matter, can be neither created nor destroyed; only converted from one form to another. A great deal of the sunlight falling on a forest will be absorbed by plants and used in photosynthetic reactions. The fuel created by that reaction will be used to support the creation of new plant material from nutrients taken from the ground. That plant material will eventually die, fall to the ground and decompose; an exothermic process which will give off in heat every calorie of radiant energy used to create it. Other portions of the infalling sunshine will evaporate water from various locations. I needn't tell you that a molecule of water vapor has more internal energy than does that same molecule in a liquid. Some might be tempted to argue that a process which reduces atmospheric water content is a cooling one, but the span of time affected by increased moisture in the air is a tiny fraction of that affected by increased CO2. The former dwarfs the latter. PS, the ground IS a thermal mass, not an absorber of thermal mass. Cornelius wrote: Are you suggesting that there is some connection? I initially wrote that neither of these had anything to do with climate change, but of course, your latter point is a critical parameter in the process. The mass of the ocean - the amount of thermal energy and dissolved CO2 it contains - has had and will continue to have an enormous impact on global warming and the Earth's climate. Cornelius wrote: That's a bit chucklable. The term "specific" in "specific heat capacity" indicates that the value (the ratio of temperature change to energy change) is specified per unit mass. Cornelius wrote: Humans live in environments ranging 230 Farenheit degrees (Omyakon, Russia to Furnace Creek, Death Valley). No one is worried about global warming reaching temperatures that would directly endanger human life. The threats that global warming presents us are all due to a rate of change with which we (and the rest of the planet) cannot cope: loss of food from crop failures and ocean acidification, loss of drinking water from snow and glacier loss and changes in rainfall patterns, flooding and wind damage from increased storm intensities and the cost of moving hundreds of millions of people to higher ground as sea levels rise worldwide. How much of that do you believe can be ameliorated by increased veganism? |
| 14-02-2015 04:40 | |
| campy☆☆☆☆☆ (8) |
The bottom line is humans will not be destroyed by the use of fossil fuels. Solar and wind are not the answer at this point in time. We can't even get an electric car to run for much more than a couple of hundred miles so there is no way our needs will be met anytime soon. I have more of a fear of a meteor striking the earth than man made global warming destroying the planet. If we can stop global warming then we should be able to reverse it, and all will be well. |
| 14-02-2015 17:04 | |
| Abraham3★★☆☆☆ (256) |
campy wrote: No one ever said they would. Some will starve. Some will die of hunger. Some will die from stronger storms and higher surges. They rest will simply have to pay the price of large mistake which could have been rectified had humanity used its head instead of its greedy little wallet with which to do its thinking. campy wrote: They are most certainly part of the answer. The rest of it includes conservation, nuclear, tidal, OTEC and hydrogen fuel cells, among other things. campy wrote: Would you care to explain why you regard a car that can run 200 miles without recharging as a failure? I drive a Hyundai Elantra that averages 32 mpg and I don't go much further than that before I start looking for a station. campy wrote: Then might I suggest you do not understand how to evaluate risks. campy wrote: We haven't even managed to slow it's acceleration, so what gives you the idea we're capable of stopping it? And even if we ceased all GHG emissions this instant, the Earth would continue to warm for another 200 years. |
| 14-02-2015 18:11 | |
| greyviper☆☆☆☆☆ (44) |
campy wrote: Yes, humans will not be easily destroyed by the use of fossil fuels. We do have adaptive mechanisms of course. Just that it's going to be harder for us to live. If Solar and Wind (and other renewables like geothermal and hydrothermal) are not the answer right now? Then what? and When? Are we going to wait until all the fossil fuels are sucked dry out of the earth? In terms of battery technology, do you think its not going to be developed and improved to a level that would certainly make them far more cheaper, far more efficient and far more environmentally friendly than they currently are? Reversing global warming would require a lot more effort and coordination than what is currently being done right now. And of course a pretty high level of technology. |
| 12-06-2015 08:32 | |
| Exodus☆☆☆☆☆ (2) |
campy wrote: I'm new too but I must disagree that the Earth has always been warming. Much the opposite, cooling to a point where the crust formed and life could evolve. Apart from the sun the internal heat helps to warm the atmosphere. The temperature of the Earth is not the crux of the matter, it's the atmospheric temperature which should concern us. Your question has no answer |
| 14-08-2015 11:08 | |
| Glitch☆☆☆☆☆ (22) |
When not in an ice-age, the Earth's mean surface temperature has been 22°C ± 1°C (with a few notable exceptions, such as the end of the Permian when mean surface temperatures soared to between 35°C and 40°C). Currently, we are in the fifth ice-age event in the last 650 million years, which has lasted for 2.58 million years. Ice-age events cause the mean surface temperature of the planet to drop by 8°C to 10°C. The current mean surface temperature of Earth is 14.8°C. It should also be noted that ice-age events have long periods of glaciation and brief interglacial periods. We are currently approaching the end of the Holocene Interglacial Period, which has been the coldest of the last eight interglacial periods. Edited on 14-08-2015 11:10 |
| 15-08-2015 17:09 | |
| Surface Detail★★★★☆ (1673) |
Glitch, could you please post your source(s) for the historical temperature data that you quote. Thank you. |
| 16-08-2015 14:37 | |
| Glitch☆☆☆☆☆ (22) |
Surface Detail wrote:  The above graph depicts the variations in the paleoclimate, with the bars at the bottom indicating the major ice-age events. The first major ice-age event (not depicted) was ~600 million years ago, pre-Cambrian. For a more detailed temperature you need to look at the specific period in question. For example, Permian paleoclimate data from fluid inclusions in halite - Chemical Geology, Volume 154, Issues 1–4, February 1999, Pages 113–132. This paper places the upper limit of the Permian temperature ranging from 21°C 270 million years ago to 50°C 250 million years ago, but most sources I have read put the maximum temperature at between 35°C and 40°C. Either way, it was still the hottest temperatures ever recorded in the last 650 million years when atmospheric CO2 levels were less than 350 ppm. The mean surface temperatures declined, and CO2 levels increased, significantly at the beginning of the Triassic when the Serbian Traps began erupting 248 million years ago. See The Triassic Paleoclimate Edited on 16-08-2015 14:58 |
| 16-08-2015 18:35 | |
| Surface Detail★★★★☆ (1673) |
Sorry, but I'm struggling to see how the graphs you posted are supposed to support your statements. For example, you writeWhen not in an ice-age, the Earth's mean surface temperature has been 22°C ± 1°C (with a few notable exceptions, such as the end of the Permian when mean surface temperatures soared to between 35°C and 40°C). but the graph shows nothing like a constant temperature at any time at any time in the Earth's history. Nor does it show an especially high temperature at the end of the Permian. Maybe you should revise your statements to better reflect the evidence? What about your stated CO2 levels? Do they accurately reflect the actual evidence? |
| 16-08-2015 22:18 | |
| Glitch☆☆☆☆☆ (22) |
Surface Detail wrote: I never said anything about Earth having a "constant" temperature. I said Earth's mean surface temperature (when not in an ice-age, and with a few notable exceptions) has been 22°C ± 1°C. Presumably you comprehend the meaning of the word "mean" or "average." You clearly did not read the paper I posted that demonstrated an extremely large spike in temperatures 250 million years ago.  With regard to atmospheric CO2 levels, they were much higher (more than 10 times current levels) before the Devonian and declined significantly during the Devonian and Carboniferous periods, reaching the their lowest level toward the end of the Permian.  |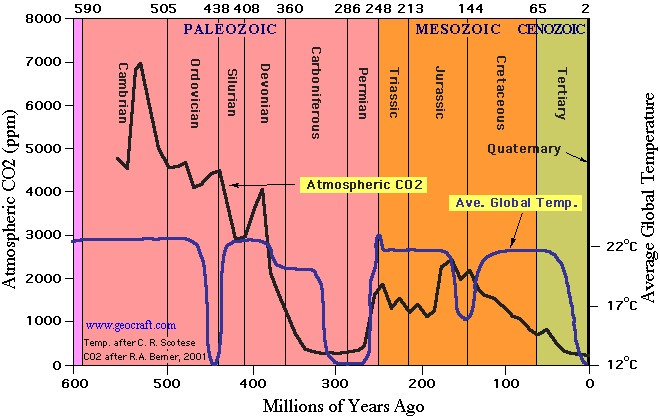
| 17-08-2015 00:04 | |
| Surface Detail★★★★☆ (1673) |
If the Earth's (mean, as in averaged over its surface) temperature has been 22°C ± 1°C for long periods, then this would be roughly constant. I don't see the temperature remaining constant to within a degree for long periods in the first graph you posted (assuming, as the literature does, that 1 ppt change in delta-O-18 represents about 1.5-2 °C change in temperature), though it does appear to do so in the second graph you posted. The temperature graphs are very different. What justification do you have for using the second one rather than the first? Where does the author of the second graph state that the graph is correct to within ± 1°C? On what proxy is the second temperature graph based? |
| 01-09-2015 13:30 | |
| abbottisgone☆☆☆☆☆ (2) |
campy wrote: You are joining issues! You are also pretending not to speak english!! You seem to like asking questions yet why do you have no answers? Most people come to a discussion meeting half-way and this is why we know you don't care what happens to our children, let alone yours. I say you are from planet accountant and are paid to maximise profits. DID YOU PERHAPS VOTE FOR COPPER INTERNET AND TRY AND HIDE THE FACT FROM YOUR FAMILY AT CHRISTMAS TIME YET STILL FIND YOURSELF FORCIBLY ISOLATED FROM SPEAKING TO THE KIDDIES!??! |
| 02-09-2015 04:42 | |
| DRKTS★★☆☆☆ (305) |
campy wrote: Hi Campy, I am new to the forum too. Your question is often used by those opposed to the AGW theory to give the impression that any temperature is Ok, so the fuss about GW is unnecessary. It is a false implication. The answer to your question is that all life forms (animals, insects, plants, etc) currently alive on the planet have evolved to exist at current temperature ranges (from typical global temperatures at the peak of the Holocene to temperature 5-10C lower at the nadir of an ice age). At the moment we are in an unusually long warm period between ice ages. If the temperature were to drop by 5C or more we would be on our way back to an ice age. If that were to happen the Earth could not support its current populations of plants or animals (or us). We know what happens then from looking back at the fossil record, there would be mass extinctions. But we have the opposite problem, we are already near or at the highest temperatures that the planet has experienced in the last million years, but our actions are pushing global temperatures into unknown territory. If it takes a 5C drop in temperature to push us into an ice age, what would adding 4C do to our world? Nobody knows but it probably is not good. We are already witnessing mass extinctions. The last time global temperatures were this high many of the current species were not around (including us). As one climatologist put it: "The climate is like a sleeping dragon, and we are experimenting on it by poking it in the eye with a sharp stick." Perhaps we should lose the stick and tiptoe away quietly to a more sustainable life style. |
| 26-09-2015 07:43 | |
IBdaMann ★★★★★(14389) |
campy wrote: Hint: There is no such thing as the earth's temperature. The side facing the sun will be warmer than the side facing away. The poles will be cooler than the equator. Our atmosphere shifts varying temperatures around the surface of the planet. The amount of atmosphere we have plays a role in the temperature at the surface. All in all, there's no way anyone can assert with any credibility that the earth is warming. In fact, for all anyone knows, the earth could be cooling right now. I don't think i can [define it]. I just kind of get a feel for the phrase. - keepit A Spaghetti strainer with the faucet running, retains water- tmiddles Clouds don't trap heat. Clouds block cold. - Spongy Iris Printing dollars to pay debt doesn't increase the number of dollars. - keepit If Venus were a black body it would have a much much lower temperature than what we found there.- tmiddles Ah the "Valid Data" myth of ITN/IBD. - tmiddles Ceist - I couldn't agree with you more. But when money and religion are involved, and there are people who value them above all else, then the lies begin. - trafn You are completely misunderstanding their use of the word "accumulation"! - Climate Scientist. The Stefan-Boltzman equation doesn't come up with the correct temperature if greenhouse gases are not considered - Hank :*sigh* Not the "raw data" crap. - Leafsdude IB STILL hasn't explained what Planck's Law means. Just more hand waving that it applies to everything and more asserting that the greenhouse effect 'violates' it.- Ceist |
| 26-09-2015 12:19 | |
| DRKTS★★☆☆☆ (305) |
IBdaMann wrote: OK there are measurements from thermometers, microwave sounders on satellites, IR imagers on satellites, radiosondes (weather balloons), plus observations of retreating glaciers, melting sea ice, melting ice caps, rising sea level, migration of planting zones poleward, tropical species invading temperate zones, later first frosts, earlier last frosts, earlier flowering seasons, longer growing seasons, increase in frequency, duration and intensity of heat waves, stronger storms, increasing humidity in the air, species extinctions, more and longer droughts, increasing wild fires, loss of multi-year ice, water shortages, ..... yeah, there's nothing to indicate the average temperature of the globe increasing if you are blind to the facts. |
| 26-09-2015 19:52 | |
| IBdaMann★★★★★ (14389) |
DRKTS wrote: Yes there are many ways that different types of measurements can be taken. No quantity of quantification methods somehow materializes into a complete dataset from which a statistically valid "average global atmospheric temperature" can be computed within any usable margin of error. ...but please, don't let me stop you from badly butchering any mathematics in your treatise of how you believe it can actually be accomplished. Please. Go ahead. I eagerly await you explanation. <evasion to occur in T - minus ... 3, ... 2, ... 1, ... now!> I don't think i can [define it]. I just kind of get a feel for the phrase. - keepit A Spaghetti strainer with the faucet running, retains water- tmiddles Clouds don't trap heat. Clouds block cold. - Spongy Iris Printing dollars to pay debt doesn't increase the number of dollars. - keepit If Venus were a black body it would have a much much lower temperature than what we found there.- tmiddles Ah the "Valid Data" myth of ITN/IBD. - tmiddles Ceist - I couldn't agree with you more. But when money and religion are involved, and there are people who value them above all else, then the lies begin. - trafn You are completely misunderstanding their use of the word "accumulation"! - Climate Scientist. The Stefan-Boltzman equation doesn't come up with the correct temperature if greenhouse gases are not considered - Hank :*sigh* Not the "raw data" crap. - Leafsdude IB STILL hasn't explained what Planck's Law means. Just more hand waving that it applies to everything and more asserting that the greenhouse effect 'violates' it.- Ceist |
| 27-09-2015 02:28 | |
| DRKTS★★☆☆☆ (305) |
IBdaMann wrote:DRKTS wrote: Read this and references therein, http://www.ncdc.noaa.gov/bams/2014 Perhaps you will learn something ... |
| 27-09-2015 02:51 | |
| IBdaMann★★★★★ (14389) |
DRKTS wrote: Read this and references therein, http://www.ncdc.noaa.gov/bams/2014 Nope. I don't read church fliers. Devoutly religious people are typically know-nothing morons who only know how to say "Go read the Bible, dude" or "Go read the Obama Administration's talking points, dude" or something equally worthless. If you've got something to say, I'll gladly listen. If you don't know of anything to say, I won't be surprised. (Hint: *YOU* are supposed to do your own research and then *YOU* post whatever insight you have to share. If you are just a moron without any insight, you might want to avoid announcing that fact by telling people to go do their own research) I don't think i can [define it]. I just kind of get a feel for the phrase. - keepit A Spaghetti strainer with the faucet running, retains water- tmiddles Clouds don't trap heat. Clouds block cold. - Spongy Iris Printing dollars to pay debt doesn't increase the number of dollars. - keepit If Venus were a black body it would have a much much lower temperature than what we found there.- tmiddles Ah the "Valid Data" myth of ITN/IBD. - tmiddles Ceist - I couldn't agree with you more. But when money and religion are involved, and there are people who value them above all else, then the lies begin. - trafn You are completely misunderstanding their use of the word "accumulation"! - Climate Scientist. The Stefan-Boltzman equation doesn't come up with the correct temperature if greenhouse gases are not considered - Hank :*sigh* Not the "raw data" crap. - Leafsdude IB STILL hasn't explained what Planck's Law means. Just more hand waving that it applies to everything and more asserting that the greenhouse effect 'violates' it.- Ceist |
| 27-09-2015 06:25 | |
| DRKTS★★☆☆☆ (305) |
IBdaMann wrote:DRKTS wrote: Read this and references therein, http://www.ncdc.noaa.gov/bams/2014 One moment you say that's just its opinion, next you are complaining that it is somebody else's research. If I take some data then its just my data who can trust that, then if I use somebody else's then who can trust that. Why don't you lay out in detail what evidence it would take to change your mind. This bring me another rock sort of argument is getting boring. |
| 27-09-2015 08:08 | |
| IBdaMann★★★★★ (14389) |
DRKTS wrote: You gibber a great deal. It is not I who has been unclear and evasive. I want only one thing: science. What I specifically don't want is religious dogma. Let's make this as easy for you as humanly possible. Question: What science have *YOU* reviewed and understand that convinced *YOU* that Global Warming is real? This should be a piece of cake. All I am asking you for is the science you insist you have. What - convinced - you? I don't think i can [define it]. I just kind of get a feel for the phrase. - keepit A Spaghetti strainer with the faucet running, retains water- tmiddles Clouds don't trap heat. Clouds block cold. - Spongy Iris Printing dollars to pay debt doesn't increase the number of dollars. - keepit If Venus were a black body it would have a much much lower temperature than what we found there.- tmiddles Ah the "Valid Data" myth of ITN/IBD. - tmiddles Ceist - I couldn't agree with you more. But when money and religion are involved, and there are people who value them above all else, then the lies begin. - trafn You are completely misunderstanding their use of the word "accumulation"! - Climate Scientist. The Stefan-Boltzman equation doesn't come up with the correct temperature if greenhouse gases are not considered - Hank :*sigh* Not the "raw data" crap. - Leafsdude IB STILL hasn't explained what Planck's Law means. Just more hand waving that it applies to everything and more asserting that the greenhouse effect 'violates' it.- Ceist |
| 27-09-2015 12:42 | |
| DRKTS★★☆☆☆ (305) |
IBdaMann wrote:DRKTS wrote: It is a combination of many things including ... My own analysis of the data. Discussions with scientists on both sides My knowledge of the Sun and the physics of the atmosphere The scientific literature My personal observations of the way that the climate is changing Now your turn, you dodged my question ... The lack of a viable alternative theory |
| 28-09-2015 01:01 | |
| IBdaMann★★★★★ (14389) |
I was very clear. I asked you for SCIENCE. specifically:IBdaMann wrote: ...but you DODGED the question without providing the SCIENCE that convinced you. You instead answered a question I did not ask: DRKTS wrote: Once again, there was no science in there. Go back and try again. I'll repeat the question for you: IBdaMann wrote: DRKTS wrote: No alternative theory is required. You don't have a viable theory in the first place. You have no falsifiable Global Warming model (that isn't false). You have no Global Warming science. All you have is religious dogma-babble that is full of violations of physics at every turn. For this there are myriads of alternative religious faiths. Pick one. If you'd like me to suggest one then perhaps you should look into fundamentalist Christianity. The faiths are isomorphic. I don't think i can [define it]. I just kind of get a feel for the phrase. - keepit A Spaghetti strainer with the faucet running, retains water- tmiddles Clouds don't trap heat. Clouds block cold. - Spongy Iris Printing dollars to pay debt doesn't increase the number of dollars. - keepit If Venus were a black body it would have a much much lower temperature than what we found there.- tmiddles Ah the "Valid Data" myth of ITN/IBD. - tmiddles Ceist - I couldn't agree with you more. But when money and religion are involved, and there are people who value them above all else, then the lies begin. - trafn You are completely misunderstanding their use of the word "accumulation"! - Climate Scientist. The Stefan-Boltzman equation doesn't come up with the correct temperature if greenhouse gases are not considered - Hank :*sigh* Not the "raw data" crap. - Leafsdude IB STILL hasn't explained what Planck's Law means. Just more hand waving that it applies to everything and more asserting that the greenhouse effect 'violates' it.- Ceist |
| 05-10-2015 12:21 | |
| Ceist★★★☆☆ (592) |
Surface Detail wrote: He is also confusing global mean surface temperature with regional water surface paleotemperature from Western Kansas in the paper he provided: http://www.sciencedirect.com/science/article/pii/S0009254198001272 Edited on 05-10-2015 13:10 |
| 05-10-2015 12:36 | |
| Ceist★★★☆☆ (592) |
The short 24 minute lecture below on the history of earth's climate is from the National Academy of Sciences 2015 Symposium by Professor Richard Alley - Geoscientist/Glaciologist. Anyone who has seen ice core graphs, has probably seen graphs based on his work. Richard Alley - 4.6 Billion Years of Earth's Climate History: The Role of CO2 https://www.youtube.com/watch?v=ujkcTZZlikg Professor Richard Alley - Curriculum Vitae http://www.geosc.psu.edu/sites/defau...long_aug13.pdf |
Join the debate Can someone answer this for me?:
Related content
| Threads | Replies | Last post |
| Global warming and the answer . | 1 | 22-09-2023 19:21 |
| The Corona Virus NCOV Event Only End After The Public Receive 2 Satisfy Answer Of The Origin & The Cu | 4 | 09-06-2021 16:22 |
| The Final Best Answer Solution For Both Climate Change & Corona Virus COVID Is Moringa Tree | 14 | 26-05-2021 06:15 |
| IPCC sucks. They have no answer for natural climatic cooling other than painting houses black to decrease | 0 | 19-04-2019 16:32 |
| Is it climate change or global warming? How science and a secret memo shaped the answer | 1 | 03-03-2019 22:20 |